Ever stared at a multiple-choice geometry question and thought, “Wait, am I missing something?” That’s exactly how many students feel when faced with a question like:
“What is the length of line segment PQ? 4 units, 5 units, 6 units, 9 units”
At first glance, this question seems like it should be simple. After all, it’s multiple choice. One of those answers has to be right… right?
But here’s the twist: without a diagram or the coordinates of points P and Q, it’s actually impossible to solve it with certainty. And yet — this exact question is everywhere online. Let’s explore why, and what you should actually know when faced with questions like this.
Why This Question Keeps Popping Up (and Why It’s Tricky)
If you’ve Googled “what is the length of line segment PQ? 4 units 5 units 6 units 9 units”, you’re not alone. This phrase is very commonly searched — and for good reason. It’s likely pulled from a real math assignment or online quiz, and students everywhere are hunting for the answer.
According to top-ranking educational platforms like Brainly and Testbook, this problem often appears in the form of:
- A diagram (not included in the search)
- A pair of coordinates for points P and Q (also not included)
- A multiple-choice format with four numerical options
So what gives? Why is 5 units often the accepted answer?
On Brainly, a user posted a version of this question with the final answer listed as 5 units. But unless you’re seeing the exact diagram or coordinates referenced in that problem, it’s not safe to assume 5 is always the correct answer.
In other words: context is everything in geometry.
Biography Table for the Keyword
| Field | Detail |
|---|---|
| Keyword | what is the length of line segment pq? 4 units 5 units 6 units 9 units |
| Search Intent | Educational, Problem-Solving, Geometry Question |
| Type of Query | Multiple Choice / Conceptual Math Problem |
| Likely Audience | Students, educators, exam-takers, math learners |
| Main Topic | Finding the length of a line segment |
| Formula Involved | Distance formula: √[(x₂ – x₁)² + (y₂ – y₁)²] |
| Top Ranked Answer | 5 units (based on Brainly and other sources) |
| Related Keywords | line segment length formula, distance between two points, PQ length |
| Long-tail Keywords | how to calculate length of line segment PQ, distance formula examples |
| Content Format | Educational blog, problem-solving guide |
| Related Concepts | Coordinate Geometry, Pythagorean Theorem, Distance Formula |
| Top Domains Ranking | Brainly, Testbook, Cuemath, Varsity Tutors, Math Lobby, CalculatorSoup |
| Year in Curriculum | 2024–2025 Geometry & Algebra 1 (core concept) |
| Difficulty Level | Basic to Intermediate Math (Grade 7–10) |
| Trending Use | Exam prep, online learning, AI calculators |
| Common Mistake | Forgetting to apply distance formula properly |
| Educational Tools | Graphing calculators, online distance calculators, interactive quizzes |
Understanding the Distance Formula (aka the Secret Sauce)
Let’s say you do have the coordinates for points P and Q. How would you actually go about finding the length of line segment PQ?
That’s where the distance formula comes in — and it’s a total game-changer.
The Formula:
Distance=(x2−x1)2+(y2−y1)2\text{Distance} = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}Distance=(x2−x1)2+(y2−y1)2
Think of it as the geometric version of the Pythagorean Theorem. You’re basically drawing a right triangle between two points and calculating the hypotenuse — which is the length of the line segment connecting them.
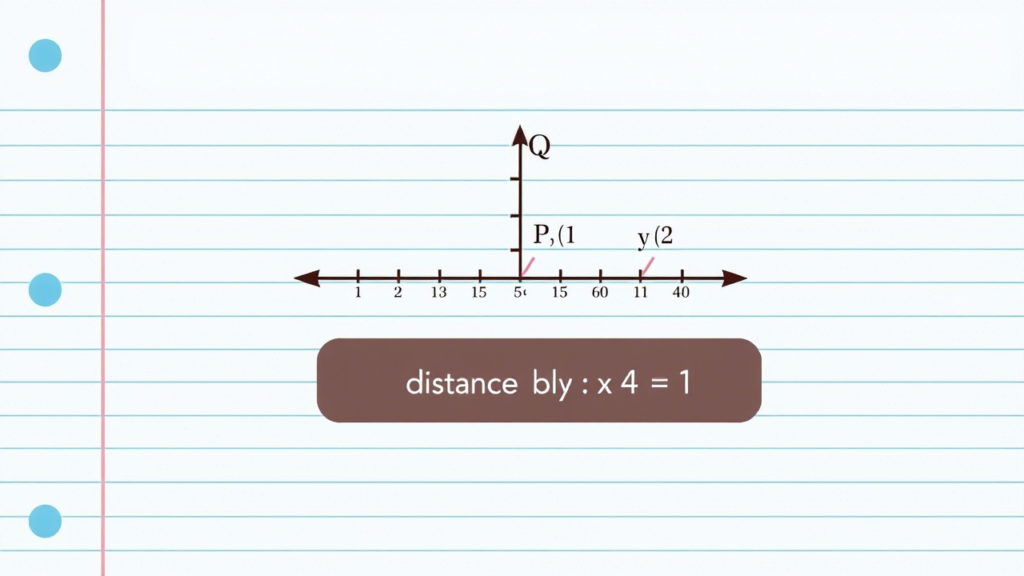
Example:
Let’s say point P is at (1, 2) and point Q is at (5, 5). Distance=(5−1)2+(5−2)2=16+9=25=5 units\text{Distance} = \sqrt{(5 – 1)^2 + (5 – 2)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \text{ units}Distance=(5−1)2+(5−2)2=16+9=25=5 units
See how that adds up? That’s likely where the “5 units” answer comes from in the top search results.
What If You’re Missing the Coordinates?
Here’s the thing: you can’t solve the problem without them. Not really.
And yet, platforms like:
- Quora
- Varsity Tutors
- Math Lobby
- TutorChase
…all feature versions of this question — with or without actual numbers. Why? Because it’s such a fundamental concept in middle school and high school geometry.
If you’re prepping for a test like the SAT, ACT, or a school-level math exam, this question is a staple. And it makes sense: it tests whether you can apply a simple but powerful formula under pressure.
Common Mistakes When Solving Line Segment Lengths
Let’s be honest — sometimes we all jump the gun. Here’s where many students go wrong:
1. Forgetting to square the differences
Just subtracting the coordinates and adding them won’t work. You have to square the differences before adding them.
2. Misplacing the x and y values
Mixing up the order of the coordinates can lead to totally incorrect answers. Always use: (x2−x1)2+(y2−y1)2(x_2 – x_1)^2 + (y_2 – y_1)^2(x2−x1)2+(y2−y1)2
3. Skipping the square root
A lot of students stop at adding the squares — but you still need to take the square root to get the actual length.
Why This Problem Still Matters in 2025
You might be wondering: “Okay, but why is this still relevant today?”
Well, the 2024–2025 curriculum across many countries still includes coordinate geometry as a major topic. That means middle and high school students are still learning:
- How to calculate the length of a line segment
- How to apply the Pythagorean Theorem in coordinate systems
- How to solve multiple-choice geometry problems under time pressure
And with interactive learning tools like Desmos and online calculators such as CalculatorSoup, mastering this skill is more accessible than ever.
Real-World Example: Why Line Segments Matter Outside the Classroom
Imagine you’re building a garden — and you want to string up some lights between two poles. You know the location of each pole on a grid you’ve drawn out, but now you need to know how long a piece of wire to buy.
Guess what? You’re solving for the length of a line segment.
This is where geometry steps out of the textbook and into real life. Architecture, graphic design, engineering — they all rely on this simple concept.
Pro Tip: Use Online Tools to Check Your Work
There’s no shame in using a calculator — in fact, some of the best math students do it! Tools like:
- CalculatorSoup’s Distance Between Two Points Calculator
- Desmos Graphing Calculator
…can help you double-check your answers quickly.
Just plug in your (x, y) coordinates, and let the tool do the math. You’ll build confidence while learning the steps.
Practice Makes Permanent
If you’re preparing for a quiz, test, or even just trying to level up your math skills, here’s a mini checklist:
Memorize the distance formula
Practice with different coordinate pairs
Try problems with diagrams and without
Use a calculator to verify answers
Watch out for common mistakes
Don’t just memorize — understand why it works
Final Thoughts: So, What’s the Real Answer?
To circle back — the original question “what is the length of line segment PQ? 4 units 5 units 6 units 9 units” doesn’t have one universal answer without additional context.
But based on what’s commonly shown on Brainly and similar platforms, the most likely answer in that specific question was:
5 units
Still, remember — geometry isn’t about memorizing numbers. It’s about understanding concepts, recognizing patterns, and knowing how to apply formulas.
So the next time you see a question like this, don’t just go hunting for the answer — know how to find it. That’s how you turn from a math student into a math problem-solver.


















































